‘Without statistics you are unlikely to find your best performance and realise consistency’

It’s easier than ever to do complex calculations and design simulations. Yet in the end it all boils down to how a design will work out of the lab, in a real product, in a real environment, according to Wendy Luiten. That’s why she’s teaching a new course called Applied statistics for R&D at High Tech Institute. ‘Statistics are often under applied, which is a pity because it can really contribute to success.’

When Wendy Luiten was taught to program, she used punch-cards that were fed into giant computers. Nowadays she can do the most complex calculations and design simulations with the press of a button on her laptop.

During Luiten’s career she witnessed an unprecedented increase in processing power. Graduating in 1984 from the University of Twente, she embarked on a distinguished career as a thermal expert and as a Six Sigma Master Black Belt at Philips. Today she works as a consultant.

That deep experience gave her a better view of statistics and computing than most engineers. New software offers great opportunities for making design simulations and Digital Twins. But the apparent ease of these new methods makes it easy to forget that a simulation is not reality. A simulation model needs to be validated to ensure that it represent reality to a sufficient degree. In addition, simulations describe an ideal world, without random variation. In the real world, random variation can make a product unreliable and disappointing to end customers.

‘Some people do not repeat, but go on a single measurement’, she says. ‘Based on that, they decide whether the design is good or not. That’s risky. You do not know how good the measurement is, you have no idea about the measurement error, you do not know how representative the prototype is, you do not know how representative the use case is.’

“Applied statistics is like driving a car, you do not need to know the working of the engine to go from A to B,” Wendy Luiten

People tend to be very optimistic about their measurement error. ‘I saw cases where people thought their measurement error was in the tenths of a degree, but a repeat measurement showed a difference of 10 degrees C. In the thermal world, that is a huge difference. So, if your repeat measurement shows such a big difference, you really cannot be sure on how well the product performs and you need to dig deeper as to the root cause for this difference.’

This is why Luiten starts her new training on Applied statistics for R&D at the High-Tech Institute with measurement statistics. In this course she will dig into key statistics skills that have shown their worth in her 30+ years of industry R&D experience. ‘First, you need to see how good your measurement is’, she explains. Then you need to be able to estimate the sample size, the number of measurements that you need to show a certain effect with sufficient probability. Once you can measure output performance accurately and with sufficient precision, you can explore different design configurations and choose the best configuration. Finally, you investigate the output mean and variation, which is ultimately how you achieve a successful design.’

Random measurement error

Luiten notes that engineers often are already aware of the systematic measurement error. ‘Systematic errors are a well-known field’, she says. ‘You can measure a golden sample and correct the results, that is a de facto calibration of your measurement. Well known, and part of many lab courses taught in higher education’.

Most people, however, don’t consider the random error or blindly use a default value of 1, 5 or 10%. But in reality, the random error depends on the measurement instrument and also on who is performing the measurements. The statistical method to find out the random error is not usually part of a lab course, so this is less common. But the first time such a test is done, the results are often surprising.’

Luiten mentions some cases she dealt with herself. ‘I have seen cases where people were confident that they had almost no random error because they had a very expensive automated measurement machine. But it turned out that the operators were making the samples in a different manner, and that caused a large random error. In another case different development labs were all claiming a 5% measurement error – but when they measured the same devices in a round robin test, there was a difference of a factor 2, because of differences in the measurement set up that were thought to be irrelevant. I have seen that apparent fluctuations in product quality could be linked to the operator performing the measurements. In all cases people were absolutely convinced that they had a negligible random error in the measurements, and these results were totally unexpected. But you only know your random error and the cause of the random error if you do the statistical test for it.’

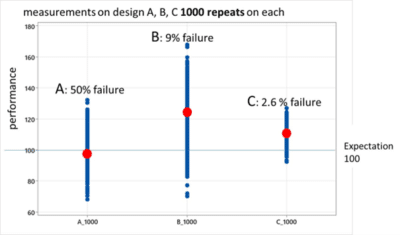
“Which design is better? Design C is preferred – Even though B has a higher average performance, C has the lowest failure rate because it performs consistently, ” Wendy Luiten

Measurement repeats

The random measurement error is especially important when it comes to so called statistical power – the probability of measuring a certain effect if it is present. If the effect you want to measure is about the same size as your measurement error, and you repeat your measurement twice, the probability of proving that effect is below 10%. So, if a design change gives you a 5C lower temperature, and your random measurement error is 5C, you will see that in 1 out of 10 measurements, and on average 9 out of 10 times the results are unconclusive, even if you do the measurement in duplicate. If you want to improve the power, you either need to lower the measurement error, or do more repeats. Sometimes people see repeat measurements as a waste of effort, but Luiten does not agree with that. ‘The true waste is to run underpowered experiments, going through all the effort of setting up and executing an experiment – and then finding out that the result is inconclusive.’

Testing different design options

Besides measurement errors and sample size estimation, a key element of the course will be testing of different designs. You can do that in hardware, but that might not be the most effective option. ‘Nowadays you can do a lot by virtual testing’, says Luiten. ‘Before you even make a prototype, you can experiment with your designs using computer simulations. Inputs can range from materials and dimensions to power and control software. You can, for example, model the impact of different materials or dimensions, or the use of a different mechanical layout, or different settings in a control algorithm. In every product there are lots of choices to be made, both on the level of the architecture and in the implementation. Finding out what inputs are the most important, and how these inputs determine your performance is key because you don’t want to realise in a later stage that an earlier decision was wrong. A Trial-and-error approach is often too expensive in time and money.’ The statistical approach is to set up a set of experiments in a special way, varying multiple inputs at the same time and not comparing single experiments but groups of experiments to tease out the effect of a single input or interactions between two inputs. This is a very powerful approach, especially in combination with computer simulations, but for a small number of inputs you can also do this in hardware. If you do the experiments in hardware, the calculated sample size from the earlier stages determines the number of repeats for the different experiments. If the experiments executed virtually, through computer simulations, the sample size is used for the validation experiments for the computer model.

Making the best choice

The next tool in the statistics toolbelt is optimization or making the best choice. Once you have found out what are the key input parameters and how they relate to the performance, you can make a data driven decision of what design configuration suits your purpose the best. Often there are multiple outputs to consider, for instance if you want high strength but at the same time low weight. Multiple Response Optimization is a well-known tool for this.

The effect of input variation

‘Once you know the impact of an input, it’s also important to look at its variation, and in turn what kind of variation it causes in the performance’, Luiten continues. ‘ This is also something that people are less familiar with but once you know how to do it this is not that difficult, and it is important. For a design to be a success, it’s not just peak performance that matters, but also that you consistently achieve that performance. Using statistical simulations tool, you can make a statistical model to link the mean and variation of your output to the statistical distribution of your inputs.

Sometimes people say that this is no use because they do not know the variation in the inputs. But if an input is important, not considering its variation is risky in terms of consistent product quality. If the statistical model shows that the input is important, you have good cause to discuss with the supplier what the distribution is and how much variation it has. This is common in automotive industry, in fact they have formal procedures in place defining exact requirements not only on the mean but also on the standard deviation of components and sub-assemblies.

Navigate the solution space

Statistical methods, in other words, help to navigate all possible configurations that together form the solution space. Luiten says “You don’t just reach your optimum performance by accident. If you have two inputs that can be high or low, that leaves four possibilities. But if you are designing something with five inputs, that leaves 32 possible configurations. And many modern-day designs have more inputs than that. And that is without even taking all the possible tolerances into account, and all different user cases. Without a structural, statistics-based approach the probability of finding optimum consistent performance is small.’

Driving cars

The components of Luiten’s course are closely interrelated, it is a chain of tools. ‘If you, for example, want to validate results, then you also need measurement statistics to tell you what your random error is. This in turn shows how large your sample needs to be, so that the experimental set up is correct. Only then can you decide whether you can trust your validation’, says Luiten.

Luiten takes a practical approach. For her, statistics is an applied skill, a means to an end. ‘Statistics in university is taught in a very theoretical way’, says Luiten. ‘I saw this in my own studies, and I saw it when my children were studying. It’s taught in a way that had limited practical use in my line of work. I compare it to driving a car: You do not need to know exactly how the engine works in order to drive from A to B. The aim of the training is not to become a statistical expert, but to be able to reach your goal with statistics.’ And mathematical tools like excel and statistics software makes application much more accessible nowadays.

Master Black belt Six Sigma

Luiten is a Master Black Belt in Design for Six Sigma, and her career has supplied her with a deep understanding and rich experience in the application of statistics in innovation processes. ‘In my experience, many engineers learn by doing, and that makes sense. You cannot learn swimming by watching the swimming Olympics, you need to get into the water yourself, even if it is only to learn how to float. So, we have practice exercises, either in excel or in a dedicated statistics tool.’ Statistics for Luiten is a general-purpose tool, and familiarity with the techniques and tools she mentions in her course is key for engineers working in a variety of fields from technical experts to designers and team leads to system architects.

‘This is a general course for people in innovation, that develop products and do research. If you measure output in continuous numerical parameters, it doesn’t matter what technical field you are in. I used these techniques in thermal applications, but any field can use them, from mechanics and electronics to optics and even software, this is mathematics. You can decide for yourself what you’ll use it for. ‘

This article is written by Tom Cassauwers, freelancer for High-Tech Systems.